Scaling models and classifiers for sparse matrix objects representing textual data in the form of a document-feature matrix. Includes original implementations of Laver', Benoit', and Garry's (2003) <doi:10.1017/S0003055403000698>, Wordscores model, the Perry and Benoit (2017) <doi:10.48550/arXiv.1710.08963> class affinity scaling model, and the Slapin and Proksch (2008) <doi:10.1111/j.1540-5907.2008.00338.x> wordfish model, as well as methods for correspondence analysis, latent semantic analysis, and fast Naive Bayes and linear SVMs specially designed for sparse textual data.

This gem removes common margin from indented strings, such as the ones produced by indented heredocs. In other words, it strips out leading whitespace chars at the beginning of each line, but only as much as the line with the smallest margin.

It is acknowledged that many strings defined by heredocs are just code and fact is that most parsers are insensitive to indentation. If, however, the strings are to be used otherwise, be it for printing or testing, the extra indentation will probably be an issue and hence this gem.

This package provides methods for analysis of energy consumption data (electricity, gas, water) at different data measurement intervals. The package provides feature extraction methods and algorithms to prepare data for data mining and machine learning applications. Deatiled descriptions of the methods and their application can be found in Hopf (2019, ISBN:978-3-86309-669-4) "Predictive Analytics for Energy Efficiency and Energy Retailing" <doi:10.20378/irbo-54833> and Hopf et al. (2016) <doi:10.1007/s12525-018-0290-9> "Enhancing energy efficiency in the residential sector with smart meter data analytics".

This package provides a fully parameterized Generalized Wendland covariance function for use in Gaussian process models, as well as multiple methods for approximating it via covariance interpolation. The available methods are linear interpolation, polynomial interpolation, and cubic spline interpolation. Moreno Bevilacqua and Reinhard Furrer and Tarik Faouzi and Emilio Porcu (2019) <url:<https://projecteuclid.org/journalArticle/Download?urlId=10.1214%2F17-AOS1652 >>. Moreno Bevilacqua and Christian Caamaño-Carrillo and Emilio Porcu (2022) <arXiv:2008.02904>. Reinhard Furrer and Roman Flury and Florian Gerber (2022) <url:<https://CRAN.R-project.org/package=spam >>.

Fits a piecewise exponential hazard to survival data using a Hierarchical Bayesian model with an Intrinsic Conditional Autoregressive formulation for the spatial dependency in the hazard rates for each piece. This function uses Metropolis- Hastings-Green MCMC to allow the number of split points to vary and also uses Stochastic Search Variable Selection to determine what covariates drive the risk of the event. This function outputs trace plots depicting the number of split points in the hazard and the number of variables included in the hazard. The function saves all posterior quantities to the desired path.

Data on standard load profiles from the German Association of Energy and Water Industries (BDEW Bundesverband der Energie- und Wasserwirtschaft e.V.) in a tidy format. The data and methodology are described in VDEW (1999), "Repräsentative VDEW-Lastprofile", <https://www.bdew.de/media/documents/1999_Repraesentative-VDEW-Lastprofile.pdf>. The package also offers an interface for generating a standard load profile over a user-defined period. For the algorithm, see VDEW (2000), "Anwendung der Repräsentativen VDEW-Lastprofile step-by-step", <https://www.bdew.de/media/documents/2000131_Anwendung-repraesentativen_Lastprofile-Step-by-step.pdf>.

The classical Markowitz's mean-variance portfolio formulation ignores heavy tails and skewness. High-order portfolios use higher order moments to better characterize the return distribution. Different formulations and fast algorithms are proposed for high-order portfolios based on the mean, variance, skewness, and kurtosis. The package is based on the papers: R. Zhou and D. P. Palomar (2021). "Solving High-Order Portfolios via Successive Convex Approximation Algorithms." <arXiv:2008.00863>. X. Wang, R. Zhou, J. Ying, and D. P. Palomar (2022). "Efficient and Scalable High-Order Portfolios Design via Parametric Skew-t Distribution." <arXiv:2206.02412>.

Calculate the injury severity score (ISS) based on the dictionary in ICDPIC from <https://ideas.repec.org/c/boc/bocode/s457028.html>. The original code was written in STATA 11'. The original STATA code was written by David Clark, Turner Osler and David Hahn. I implement the same logic for easier access. Ref: David E. Clark & Turner M. Osler & David R. Hahn, 2009. "ICDPIC: Stata module to provide methods for translating International Classification of Diseases (Ninth Revision) diagnosis codes into standard injury categories and/or scores," Statistical Software Components S457028, Boston College Department of Economics, revised 29 Oct 2010.

The ultimate goal is to support 2-2-1, 2-1-1, and 1-1-1 models for multilevel mediation, the option of a moderating variable for either the a, b, or both paths, and covariates. Currently the 1-1-1 model is supported and several options of random effects; the initial code for bootstrapping was evaluated in simulations by Falk, Vogel, Hammami, and MioÄ eviÄ (2024) <doi:10.3758/s13428-023-02079-4>. Support for Bayesian estimation using brms comprises ongoing work. Currently only continuous mediators and outcomes are supported. Factors for any predictors must be numerically represented.

The ClusterSignificance package provides tools to assess if class clusters in dimensionality reduced data representations have a separation different from permuted data. The term class clusters here refers to, clusters of points representing known classes in the data. This is particularly useful to determine if a subset of the variables, e.g. genes in a specific pathway, alone can separate samples into these established classes. ClusterSignificance accomplishes this by, projecting all points onto a one dimensional line. Cluster separations are then scored and the probability of the seen separation being due to chance is evaluated using a permutation method.

Rapid is a Go library for property-based testing.

Rapid checks that properties you define hold for a large number of automatically generated test cases. If a failure is found, rapid automatically minimizes the failing test case before presenting it.

Features:

• imperative Go API with type-safe data generation using generics

• data generation biased to explore "small" values and edge cases more thoroughly

• fully automatic minimization of failing test cases

• persistence and automatic re-running of minimized failing test cases

• support for state machine ("stateful" or "model-based") testing

• no dependencies outside the Go standard library

This package provides several measures ((dis)similarity, distance/metric, correlation, entropy) for comparing two partitions of the same set of objects. The different measures can be assigned to three different classes: Pair comparison (containing the famous Jaccard and Rand indices), set based, and information theory based. Many of the implemented measures can be found in Albatineh AN, Niewiadomska-Bugaj M and Mihalko D (2006) <doi:10.1007/s00357-006-0017-z> and Meila M (2007) <doi:10.1016/j.jmva.2006.11.013>. Partitions are represented by vectors of class labels which allow a straightforward integration with existing clustering algorithms (e.g. kmeans()). The package is mostly based on the S4 object system.

This plugin goes to great lengths to save and restore all the details from your tmux environment. Here's what's been taken care of:

• all sessions, windows, panes and their order

• current working directory for each pane

• exact pane layouts within windows (even when zoomed)

• active and alternative session

• active and alternative window for each session

• windows with focus

• active pane for each window

• "grouped sessions" (useful feature when using tmux with multiple monitors)

• programs running within a pane! More details in the restoring programs doc.

Optional:

• restoring vim and neovim sessions

• restoring pane contents

Two arms clinical trials required sample size is calculated in the comprehensive parametric context. The calculation is based on the type of endpoints(continuous/binary/time-to-event/ordinal), design (parallel/crossover), hypothesis tests (equality/noninferiority/superiority/equivalence), trial arms noncompliance rates and expected loss of follow-up. Methods are described in: Chow SC, Shao J, Wang H, Lokhnygina Y (2017) <doi:10.1201/9781315183084>, Wittes, J (2002) <doi:10.1093/epirev/24.1.39>, Sato, T (2000) <doi:10.1002/1097-0258(20001015)19:19%3C2689::aid-sim555%3E3.0.co;2-0>, Lachin J M, Foulkes, M A (1986) <doi:10.2307/2531201>, Whitehead J(1993) <doi:10.1002/sim.4780122404>, Julious SA (2023) <doi:10.1201/9780429503658>.

Calculates sample size for various scenarios, such as sample size to estimate population proportion with stated absolute or relative precision, testing a single proportion with a reference value, to estimate the population mean with stated absolute or relative precision, testing single mean with a reference value and sample size for comparing two unpaired or independent means, comparing two paired means, the sample size For case control studies, estimating the odds ratio with stated precision, testing the odds ratio with a reference value, estimating relative risk with stated precision, testing relative risk with a reference value, testing a correlation coefficient with a specified value, etc. <https://www.academia.edu/39511442/Adequacy_of_Sample_Size_in_Health_Studies#:~:text=Determining%20the%20sample%20size%20for,may%20yield%20statistically%20inconclusive%20results.>.

Computation of sparse portfolios for financial index tracking, i.e., joint selection of a subset of the assets that compose the index and computation of their relative weights (capital allocation). The level of sparsity of the portfolios, i.e., the number of selected assets, is controlled through a regularization parameter. Different tracking measures are available, namely, the empirical tracking error (ETE), downside risk (DR), Huber empirical tracking error (HETE), and Huber downside risk (HDR). See vignette for a detailed documentation and comparison, with several illustrative examples. The package is based on the paper: K. Benidis, Y. Feng, and D. P. Palomar, "Sparse Portfolios for High-Dimensional Financial Index Tracking," IEEE Trans. on Signal Processing, vol. 66, no. 1, pp. 155-170, Jan. 2018. <doi:10.1109/TSP.2017.2762286>.

This package provides a simple interface to the Geographic Header information from the "2010 US Census Summary File 2". The entire Summary File 2 is described at <https://catalog.data.gov/dataset/census-2000-summary-file-2-sf2>, but note that this package only provides access to parts of the geographic header ('geoheader') of the file. In particular, only the first 101 columns of the geoheader are included and, more importantly, only rows with summary levels (SUMLEVs) 010 through 050 (nation down through county level) are included. In addition to access to (part of) the geoheader, the package also provides a decode function that takes a column name and value and, for certain columns, returns "the meaning" of that column (i.e., a "SUMLEV" value of 40 means "State"); without a value, the decode function attempts to describe the column itself.

Allows for data to be transformed before using it to construct models. Builds structures to allow functions in the PMML package to output transformation details in addition to the model in the resulting PMML file. The Predictive Model Markup Language (PMML) is an XML-based language which provides a way for applications to define machine learning, statistical and data mining models and to share models between PMML compliant applications. More information about the PMML industry standard and the Data Mining Group can be found at <http://www.dmg.org>. The generated PMML can be imported into any PMML consuming application, such as Zementis Predictive Analytics products, which integrate with web services, relational database systems and deploy natively on Hadoop in conjunction with Hive, Spark or Storm, as well as allow predictive analytics to be executed for IBM z Systems mainframe applications and real-time, streaming analytics platforms.

An exact method for computing the Poisson-Binomial Distribution (PBD). The package provides a function for generating a random sample from the PBD, as well as two distinct approaches for computing the density, distribution, and quantile functions of the PBD. The first method uses direct-convolution, or a dynamic-programming approach which is numerically stable but can be slow for a large input due to its quadratic complexity. The second method is much faster on large inputs thanks to its use of Fast Fourier Transform (FFT) based convolutions. Notably in this case the package uses an exponential shift to practically guarantee the relative accuracy of the computation of an arbitrarily small tail of the PBD -- something that FFT-based methods often struggle with. This ShiftConvolvePoiBin method is described in Peres, Lee and Keich (2020) <arXiv:2004.07429> where it is also shown to be competitive with the fastest implementations for exactly computing the entire Poisson-Binomial distribution.

__This package is deprecated__. Please, use genByteString from the [random package (version >=1.2)](https://hackage.haskell.org/package/random) instead. . Efficient generation of random bytestrings. The implementation populates uninitialized memory with uniformily distributed random 64 bit words (and 8 bit words for remaining bytes at the end of the bytestring). . Random words are generated using the PRNG from the [mwc-random](https://hackage.haskell.org/package/mwc-random) package or the [pcg-random](https://hackage.haskell.org/package/pcg-random) package. It is also possible to use a custom PRNG by providing an instance for the RandomWords type class and using the function generate from the module "Data.ByteString.Random.Internal". . The generated byte strings are suitable for statistical applications. They are /not/ suitable for cryptographic applications. .  .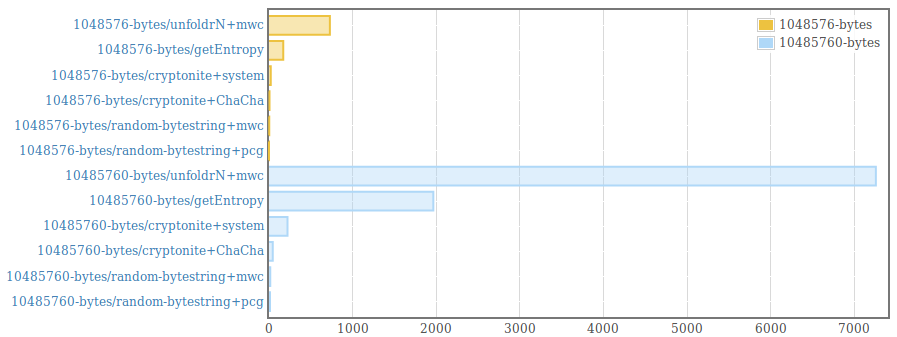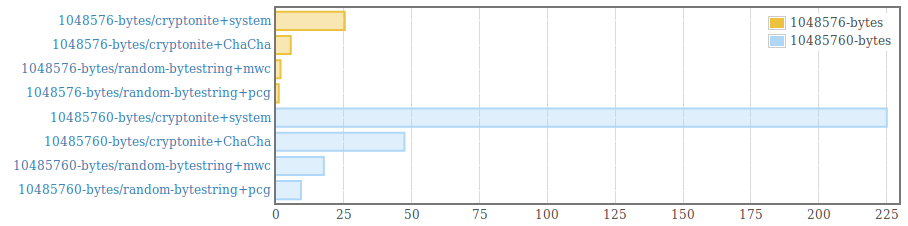 

The Importance Index (I.I.) can determine the loss and solution sources for a system in certain knowledge areas (e.g., agronomy), when production (e.g., fruits) is known (Demolin-Leite, 2021). Events (e.g., agricultural pest) can have different magnitudes (numerical measurements), frequencies, and distributions (aggregate, random, or regular) of event occurrence, and I.I. bases in this triplet (Demolin-Leite, 2021) <https://cjascience.com/index.php/CJAS/article/view/1009/1319>. Usually, the higher the magnitude and frequency of aggregated distribution, the greater the problem or the solution (e.g., natural enemies versus pests) for the system (Demolin-Leite, 2021). However, the final production of the system is not always known or is difficult to determine (e.g., degraded area recovery). A derivation of the I.I. is the percentage of Importance Index-Production Unknown (% I.I.-PU) that can detect the loss or solution sources, when production is unknown for the system (Demolin-Leite, 2024) <DOI:10.1590/1519-6984.253218>.

This package provides methods for model-based clustering of multinomial counts under the presence of covariates using mixtures of multinomial logit models, as implemented in Papastamoulis (2023) <DOI:10.1007/s11634-023-00547-5>. These models are estimated under a frequentist as well as a Bayesian setup using the Expectation-Maximization algorithm and Markov chain Monte Carlo sampling (MCMC), respectively. The (unknown) number of clusters is selected according to the Integrated Completed Likelihood criterion (for the frequentist model), and estimating the number of non-empty components using overfitting mixture models after imposing suitable sparse prior assumptions on the mixing proportions (in the Bayesian case), see Rousseau and Mengersen (2011) <DOI:10.1111/j.1467-9868.2011.00781.x>. In the latter case, various MCMC chains run in parallel and are allowed to switch states. The final MCMC output is suitably post-processed in order to undo label switching using the Equivalence Classes Representatives (ECR) algorithm, as described in Papastamoulis (2016) <DOI:10.18637/jss.v069.c01>.

This package performs estimation and inference on a partially missing target outcome (e.g. gene expression in an inaccessible tissue) while borrowing information from a correlated surrogate outcome (e.g. gene expression in an accessible tissue). Rather than regarding the surrogate outcome as a proxy for the target outcome, this package jointly models the target and surrogate outcomes within a bivariate regression framework. Unobserved values of either outcome are treated as missing data. In contrast to imputation-based inference, no assumptions are required regarding the relationship between the target and surrogate outcomes. Estimation in the presence of bilateral outcome missingness is performed via an expectation conditional maximization either algorithm. In the case of unilateral target missingness, estimation is performed using an accelerated least squares procedure. A flexible association test is provided for evaluating hypotheses about the target regression parameters. For additional details, see: McCaw ZR, Gaynor SM, Sun R, Lin X: "Leveraging a surrogate outcome to improve inference on a partially missing target outcome" <doi:10.1111/biom.13629>.

Derivation tree operations are needed for implementing grammar-based genetic programming and grammatical evolution: Generating a random derivation trees of a context-free grammar of bounded depth, decoding a derivation tree, choosing a random node in a derivation tree, extracting a tree whose root is a specified node, and inserting a subtree into a derivation tree at a specified node. These operations are necessary for the initialization and for decoders of a random population of programs, as well as for implementing crossover and mutation operators. Depth-bounds are guaranteed by switching to a grammar without recursive production rules. For executing the examples, the package BNF is needed. The basic tree operations for generating, extracting, and inserting derivation trees as well as the conditions for guaranteeing complete derivation trees have been presented in Geyer-Schulz (1997, ISBN:978-3-7908-0830-X). The use of random integer vectors for the generation of derivation trees has been introduced in Ryan, C., Collins, J. J., and O'Neill, M. (1998) <doi:10.1007/BFb0055930> for grammatical evolution.